Transitions de phase d'un corps pur
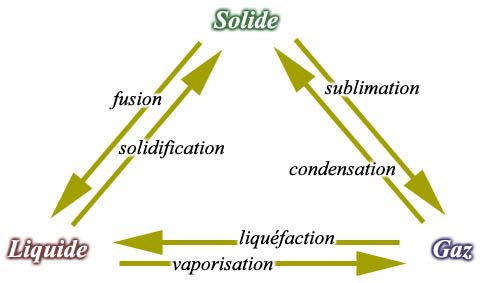
Définitions
\(\triangleright\) Définition d'une propriété allotropique
Un corps est dit allotropique lorsqu'il peut se mettre dans différentes phases aux propriétés différentes
Equation d'état de Van der Waals
Diagrammes
\(\triangleright\) Courbe de saturation
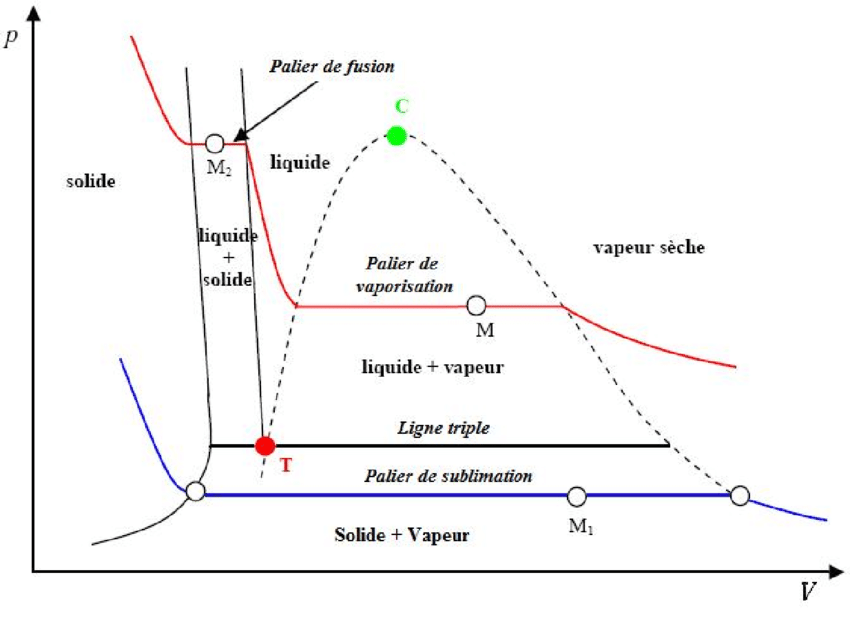
La courbe en pointillés représente la courbe de saturation.
Elle nous donne la répartition des coexistences de phases.
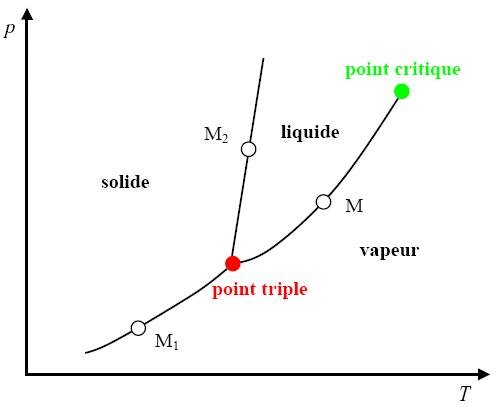
\(\triangleright\) Diagramme de phase
Critères de stabilité
Critères de stabilité des étatsEtats métastables
Sens d'évolution
\(\triangleright\) Evolution dans un système hors équilibre
Si un système hors équilibre \(dG\lt 0\) est composé de plusieurs phases, alors le système évolue de telle sorte que la phase ayant l'enthalpie libre la plus grande diminue au profit des phases ayant une enthalpie inférieur.
Soient 2 phases de quantité \(n_1\) et \(n_2\), et d'enthalpie libre molaire \(g_1,g_2\). La transition est toujours à \(P\) et \(T\) constants (transition de phase).
L'équilibre est présent lorsque les enthalpies sont : \({{g_1=g_2}}\).
Théorème des moments
Fraction molaireThéorème des moments
Transition de phase
Transition de phase du \(1er\) ordre
\(\triangleright\) Définition de la transition de phase du \(1er\) ordre
Les transitions de phase du \(1er\) ordre sont celles caractérisées par une variation continue de l'Enthalpie libre \(g\) et discontinue des ses dérivées premières.
Chaleur latente
Transition de phase du \(2ème\) ordre
\(\triangleright\) Définition d'une transition de phase du \(2ème\) si:
- l'Enthalpie libre molaire \(g\) et ses dérivées premières sont continues
- les dérivés de \(g\) d'ordre supérieures sont discontinues
Remarques
\(\triangleright\) Remarque sur les transitions phase
Toutes les transitions de phase ont lieu à pression et à température constante
On utilise donc \(G\) lEnthalpie libre pour les décrire
Lorsqu'il y a coexistence de plusieurs phases dans un système, on s'intéresse à la
Variance thermodynamique pour déterminer le nombre de variable intensive dont nous avons besoin pour décrire ce système


